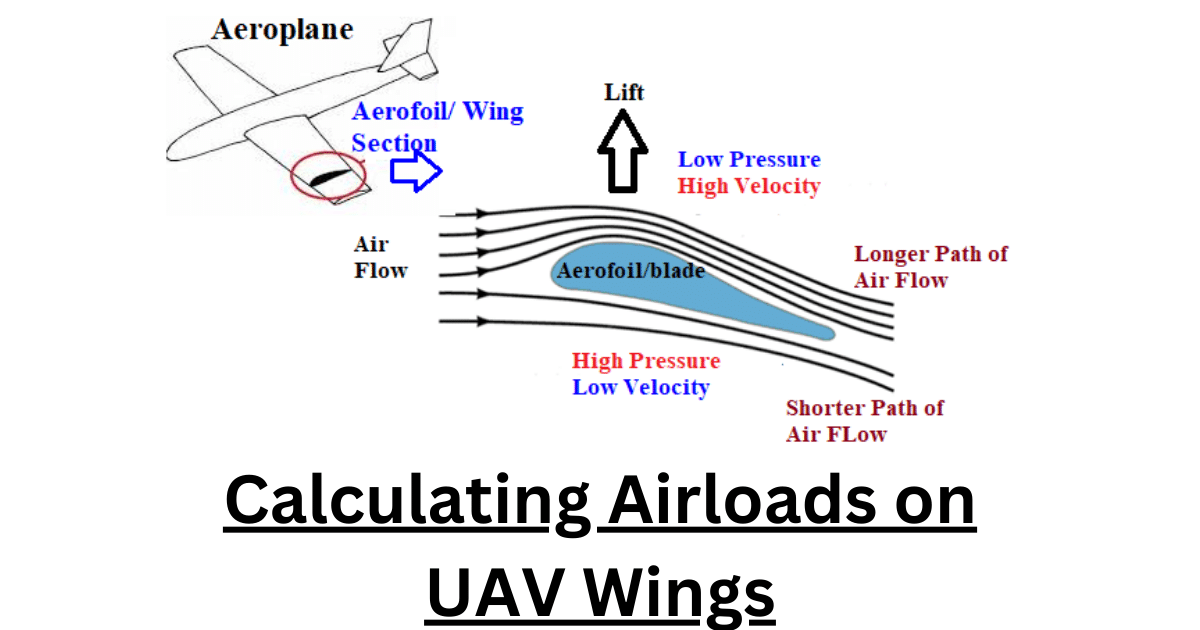
Introduction
The dream of flight has always captivated human imagination, and in the realm of Unmanned Aerial Vehicles (UAVs), this dream has evolved into a dynamic reality. At the core of a UAV's ability to navigate the skies lies the intricate science of calculating airloads on its wings. In this comprehensive exploration, we will delve into the multifaceted world of UAV aerodynamics, uncovering the principles and calculations behind the forces that propel these unmanned marvels through the air.
Nowadays modern wind tunnels have decreased the load work of load group as they are more accurate and time efficient. But loads estimation is still important because the faulty assumptions can lead to failure of aircraft when the real load is applied.
The Foundations of UAV Aerodynamics
- Lift and Drag: The Yin and Yang of Flight
Before we embark on the journey of calculating airloads, let's acquaint ourselves with the foundational principles of aerodynamics—lift and drag. Lift is the force that enables an aircraft, or in this case, a UAV, to ascend into the sky. It is counteracted by drag, the aerodynamic force resisting forward motion through the air. Achieving a delicate equilibrium between lift and drag is the key to efficient and controlled flight.
- The Wing's Role in UAV Flight
The UAV wing, analogous to an aircraft's wing, is a pivotal component in generating lift. Its design is a careful interplay of various factors, including the airfoil shape, angle of attack, and wing area. These elements collectively determine how the UAV interacts with the air, dictating its ability to soar gracefully or navigate with precision.
Understanding the Lift Equation
- The Lift Equation Unveiled
The lift equation is the cornerstone of understanding how UAVs, like their manned counterparts, harness aerodynamics to achieve flight. Mathematically expressed as:
L=0.5×Cl×ρ×V2×S
Where:
- L is the lift force,
- Cl is the coefficient of lift,
- ρ represents air density,
- V is the velocity of the UAV relative to the air,
- S is the wing area.
This equation underscores the dependency of lift on airspeed, air density, wing area, and the specific characteristics of the wing's airfoil.
- Coefficient of Lift and its Influences
The coefficient of lift (Cl) is a pivotal factor in the lift equation. It is influenced by the UAV's wing design, including the airfoil shape and angle of attack. Engineers meticulously tailor these design elements to optimize lift and ensure the UAV's ability to overcome gravitational forces.
Drag Equation: Navigating Resistance
While lift propels the UAV skyward, drag seeks to impede its progress. The drag equation is instrumental in quantifying this resistance:
D=0.5×Cd×ρ×V2×A
Where:
- D is the drag force,
- Cd is the coefficient of drag.
Much like the coefficient of lift, Cd hinges on the UAV's aerodynamic characteristics. Reducing drag is a perpetual pursuit in UAV design, aiming to enhance overall efficiency and extend operational range.
Air Loads
The loads which an aircraft encounters during flight are termed as the air loads, which include manoeuvre and gust loads. Analysis of air loads can be displayed using a V-n diagram.
- Maneuver Loads
The greatest air loads on an aircraft usually come from the generation of lift during high-g manoeuvres or in response to an extreme gust. Aircraft load factor ‘n’ represents the manoeuvring of aircraft as multiple of acceleration due to gravity. At lower speeds the highest load factor an aircraft can experience is limited by the maximum lift available. At higher speeds the maximum load factor is limited to some arbitrary value based upon the expected use of the aircraft. Generally, fighters have higher load factors due to their manoeuvrability whereas transport aircrafts and strategic bombers have lower load factors due to their controllability. Maneuver loads are defined by the stall limit, the positive and negative load factor limits and the dynamic pressure limit. The limit load factors for aircraft are set according to Military or civil aviation standards considering the use of the aircraft. The stall limit is given as:
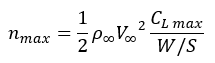
Where:
- nmax is the drag force,
- ρ represents air density,
- Clmax is the maximum coefficient of lift,
- V is the velocity of the UAV relative to the air,
- S is the wing area,
- W/S is the wing loading of the aircraft.
- Gust Loads
The loads experienced by aircraft when it encounters a strong gust can exceed the manoeuvre loads in some cases. When an aircraft experiences a gust, the effect is an increase or decrease in the angle of attack. The following figure demonstrates an aircraft experiencing an upward gust with velocity ‘U’. The change in angle of attack is approximately U divided by the aircraft velocity ‘V’. The change in angle of attack is in the upward direction.
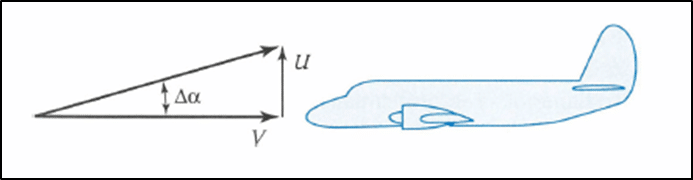
The resulting change in load factor can be derived as,
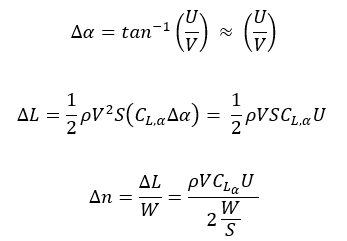
the above equation assume that the aircraft instantly encounters the gust and that it instantly affects the entire aircraft. These assumptions are unrealistic. In reality gust tends to follow a cosine like intensity as the aircraft flies through. This reduces the aircraft acceleration up to 40%. To account for this effect, a statistical gust alleviation factor K is defined which is then multiplied with the measured gust velocity Ude to give the gust velocity as,
U=KUde
Where K for subsonic aircraft, is given by the following equation,
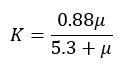
Where μ is he mass ratio and is given by the following equation,
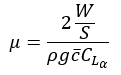
Using these equations, gust speeds and the change in load factors due to these gusts are calculated at 3 points in flight to satisfy military and civil aviation requirements i.e., at cruise, max turbulence and at dive speed.
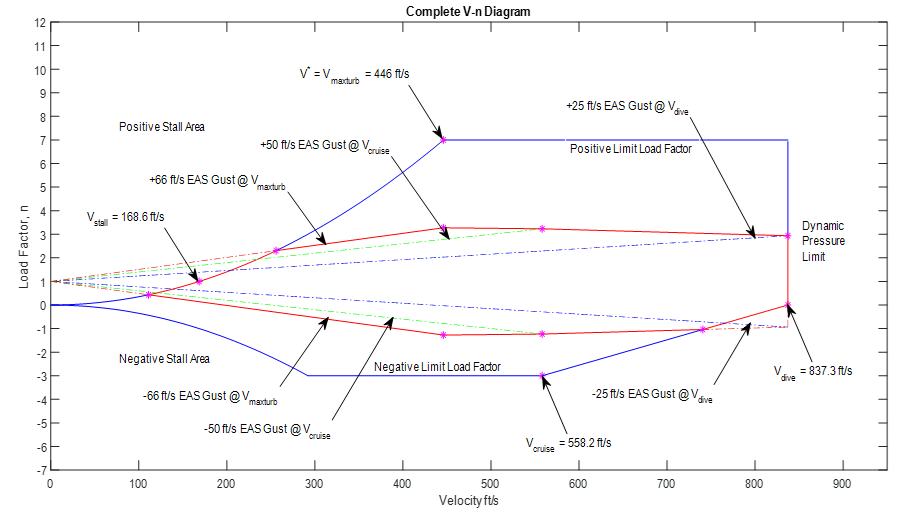
- Vn Diagram
A V-n diagram is then constructed to depict the maneuver loads coupled with the gust loads.
UAV Weight: A Critical Consideration
The weight of the UAV is a defining factor in the aerodynamic equation. The lift force must equal or exceed the UAV's weight for it to achieve and sustain flight. Changes in weight, whether due to payload adjustments or fuel consumption, necessitate constant recalibration of the aerodynamic forces at play.
Computational Tools: Bridging Theory and Reality
In the pursuit of precision and reliability, engineers leverage advanced computational tools. Computational Fluid Dynamics (CFD) simulations and wind tunnel testing provide nuanced insights into UAV aerodynamics. These tools allow for in-depth analyses, enabling designers to refine wing shapes, optimize control surfaces, and enhance overall UAV performance.
Case Studies: Real-World Applications
To contextualize the theoretical aspects discussed, let's delve into a couple of real-world case studies where the principles of calculating airloads on UAV wings have been applied:
A. Surveillance UAVs: Balancing Payload and Efficiency
Surveillance UAVs are tasked with monitoring vast areas, often carrying sophisticated payloads. Calculating airloads is pivotal in designing wings that can lift the necessary equipment while maintaining optimal efficiency. The ability to hover and navigate with minimal drag is particularly crucial for prolonged surveillance missions.
B. Delivery Drones: Navigating Urban Skies
Delivery drones operate in complex urban environments, requiring precise control over lift and drag. The aerodynamic considerations extend beyond the traditional flight envelope, with the need for rapid ascents and descents. Calculating airloads becomes a dynamic process, adapting to the changing demands of the delivery mission.
The Future of UAV Aerodynamics
As technology continues to advance, the field of UAV aerodynamics evolves in tandem. Future innovations may involve the integration of artificial intelligence for real-time aerodynamic adjustments, morphing wing technologies that adapt to varying flight conditions, and enhanced materials that reduce weight while maintaining structural integrity.
Conclusion: Decoding the Symphony of UAV Flight
In conclusion, calculating airloads on UAV wings is a multidimensional orchestration of aerodynamic principles, mathematical formulas, and real-world applications. The dance between lift and drag, the finesse of angle of attack adjustments, and the adaptability to changing air conditions collectively define the symphony of UAV flight. From the early pioneers of aviation to the cutting-edge UAVs navigating our skies today, the pursuit of mastering flight remains an enduring testament to human ingenuity. As we continue to push the boundaries of what is possible, the intricate calculations behind UAV airloads serve as a compass guiding us toward new heights in unmanned flight.